Question

The range of the function f(k) = k2 + 2k + 1 is {25, 64}. What is the function’s domain?

Answer 1

The domain of a function contains the x-values of the function while the range of the function contains the y-values of the function. In this case, we substitute 25 and 64 to y. Then,
25 = k2 + 2 k + 1 (k-4) * (k+6) = 0
64 = k2 + 2 k + 1 (k-7) * (k+9) = 0
hence the domain is {-9,-6, 4,7}

Answer 2

Domain is [-9,-6] U [4,7]

Explanation:

`f(k) = k^2 + 2k + 1`

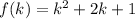
Range is {25, 64}. Range is the y value

LEts plug in 25 for f(k) and solve for k

`25 = k^2 + 2k + 1`

Subtract 25 on both sides

`0= k^2 + 2k -24`

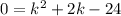
Product is -24 and sum is +2. factors are 6 and -4

`0= (k+6)(k-4)`

`k+6=0, k=-6`

`k-4=0, k=4`

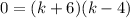
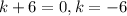
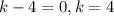
Do the same and solve for x when f(x)= 64

`64 = k^2 + 2k + 1`

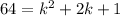
Subtract 64 on both sides

`0= k^2 + 2k -63`

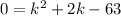
Product is -63 and sum is +2. factors are 9 and -7

`0= (k+9)(k-7)`

`k+9=0, k=-9`

`k-7=0, k=7`

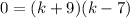
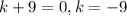
We got k values, -9,-6,4,7

Domain is [-9,-6] U [4,7]