Question

Newton’s law of cooling states that the temperature of an object changes at a rate proportional to the difference between its temperature and that of its surroundings. Suppose that the temperature of a cup of coffee obeys Newton’s law of cooling. If the coffee has a temperature of 200◦F when freshly poured, and 1 min later has cooled to 190◦F in a room at 70◦F, determine when the coffee reaches a temperature of 150◦F.

Answer 1

Let T represent the temperature of the object

Let To represent the temperature of the surroundings

Newton’s law of cooling states that the temperature of an object changes at a rate proportional to the difference between its temperature and that of its surroundings. This can be expressed as

`(dT)/(dt)\text{ = }-\text{ k}(T-T_o)`

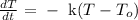
k is a constant and it is negative because the temperature is reducing. The next step is to separate the variables. We have

`\begin{gathered} \frac{dT}{(T\text{ - To)}}\text{ = - kdt} \\ By\text{ integrating both sides, we have} \\ \int \frac{dT}{T\text{ - To}}\text{ = }\int -\text{ kdt} \\ \ln \text{ }\lvert T-To\rvert\text{ = }-\text{ kt + C} \end{gathered}`

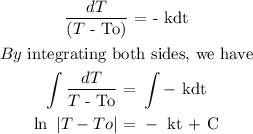
Taking the exponents of both sides, it becomes

`e^(\ln \lvert T-To\rvert)=e^{(-\text{ kt + }C)}`

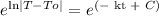
By applying the rules of logarithms and exponents,

e^ln = 1

a^(m + n) = a^ma^n

Thus, the equation becomes

`\begin{gathered} T-To=e^(-kt)e^C \\ \text{Let e}^C\text{ = A} \\ \text{Thus, we have} \\ T-To=Ae^{-\text{ kt}} \\ T=Ae^{-\text{ kt}}\text{ + To} \end{gathered}`

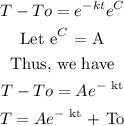
We would apply this formula in solving the given problem. From the information given,

To = 70, Intial temrperature when time, t = 0 is 200

After 1 min, t = 1, T = 190

We would calculate the value of A and k. We have

For t = 0,

200 = Ae^- (k * 0) + 70

200 = Ae^0 + 70

200 = A + 70

A = 200 - 70 = 130

The equation becomes

T = 130e^- kt + 70

Substituting T = 190 and t = 1, it becomes

190 = 130e^- k(1) + 70

190 = 130e^- k + 70

190 - 70 = 130e^- k

120 = 130e^- k

120/130 = e^- k

Taking the natural log of both sides,

ln (120/130) = ln e^- k

ln e = 1

ln (120/130) = - k

k = ln (120/130)/- 1

k = 0.08

Therefore, the equation would be

`T=130e^{-\text{ 0.08t}}\text{ + 70}`

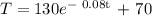
We want to find t when T = 150. By substituting T = 150 into the formula, we have

150 = 130e^- 0.08t + 70

150 - 70 = 130e^- 0.08t

80 = 130e^- 0.08t

80/130 = e^- 0.08t

Taking the natural log of both sides,

ln 80/130 = ln e^- 0.08t

ln 80/130 = - 0.08t

t = (ln 80/130 )/(- 0.08)

t = 6.07 mins