Question

The point in the third quadrant corresponds to angle θ on the unit circle. What is the value of sec θ and the value of cot θ?

Answer 1

The value of sec 0 and the value of cot 0 would be: -5/3 & 3/4.

How? Example:

cos(x) = -3/5

sin(x) = -√(1² -(-3/5)² = -4/5

sec(x) = 1/ cos(x) = 1/ -(3/8) = -5/3

cot(x) = cos(x)/sin(x) =(-3/5)/(-4/5) = 3/4

Answer 2

sec θ = -5/3

cot θ = -3/4

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one.

The point (-3/5,y) in the third quadrant corresponds to angle θ on the unit circle. What is the value of sec θ and the value of cot θ?

My answer:

x -coordinate: -3/5

hypotenuse in this situation is 1 because it is the radius of the unit circle.

As we know:

• sec θ= 1 / cos θ = hypotenuse / x -coordinate

<=> sec θ= 1 / (-3/5) = -5/3

• cot θ = 1 / tan θ = x-coordinate / y - coordinate

<=> cot θ = -3/5 / y

`y^2 + (-3/5)^2 = 1`

<=>
`y^2 = 1 -(-3/5)^2`

<=>
`y^(2) = (16)/(25)`

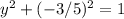
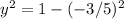
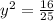
<=> y = 4/5 or y = -4/5

But The point in the third quadrant => y = 4/5

So cot θ = -3/5 / 4/5 = -3/4