Answer:
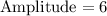

Domain:
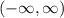
Range:
![[-6,6]](https://img.qammunity.org/2018/formulas/mathematics/high-school/9uapl2h93auy8ezv30gsuizj7woqd6174l.png) .
.
Explanation:
We have been given formula of trigonometric function
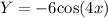 .
.
We know that equation of a cosine function is
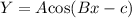 , where,
, where,
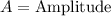 ,
,
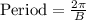
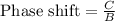
Upon looking at our given function we can see that amplitude of our given function is 6.
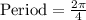

Therefore, the period of our given function is
 .
.
Since the basic cosine function is defined for all x values and it has no domain constraints, therefore, the domain of our given function will be
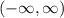 .
.
We know that the range of basic cosine function is
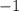 to 1 or
to 1 or
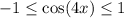 .
.
Upon multiplying the edges of range by
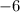 we will get,
we will get,
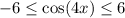
Therefore, the range of our given function is
![[-6,6]](https://img.qammunity.org/2018/formulas/mathematics/high-school/9uapl2h93auy8ezv30gsuizj7woqd6174l.png) .
.