Question

Which table represents a nonlinear function? x y 2 -9 4 1 6 11 x y 2 -14 4 -16 6 -18 x y 2 0 4 6 6 16 x y 2 -9 4 -6 6 -3

Answer 1

Answer: The third table represents a nonlinear function

x y

2 0

4 6

6 16

Explanation:

We know that for a nonlinear function, the rate of change of y is not constant w.r.t x.

The rate of change of y w.r.t. x is given by :-

`\frac{\text{Change in y}}{\text{Change in x}}`

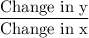
For Table 1.

The rate of change of function is given by :_

`(1-(-9))/(4-2)=(10)/(2)=5`

`(11-1)/(6-4)=(10)/(2)=5`

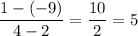
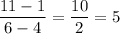
Thus , the rate of change is constant through out the function, hence it is not representing a nonlinear function.

For Table 2.

The rate of change of function is given by :_

`(-16-(-14))/(4-2)=(-2)/(2)=-1`

`(-18-(-16))/(6-4)=(-2)/(2)=-1`

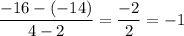
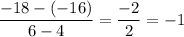
Thus , the rate of change is constant through out the function, hence it is not representing a nonlinear function.

For Table 3.

The rate of change of function is given by :_

`(6-0)/(4-2)=(6)/(2)=3`

`(16-6)/(6-4)=(10)/(2)=5`

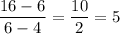
Thus , the rate of change is not constant through out the function, hence it is representing a nonlinear function.

For Table 4.

The rate of change of function is given by :_

`(-6-(-9))/(4-2)=(3)/(2)`

`(-3-(-6))/(6-4)=(3)/(2)`

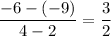
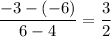
Thus , the rate of change is constant through out the function, hence it is not representing a nonlinear function.

Answer 2

The Third one, Y jumps from 0 to 6 then 16