Question

What value represents the vertical translation from the graph of the parent function f(x) = x2 to the graph of the function

g(x) = (x + 5)2 + 3?

Answer 1

the +3 is the vertical and the +5 tells you horizontal. so this graph moves 3 up and 5 left. But since it only wants vertical that would be the +3

Answer 2

Shifted 3 units upwards.

Explanation:

We have been given a parent function
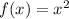`f(x)=x^2` and a translated function
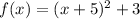`f(x)=(x+5)^2+3`. We are asked to determine the vertical translation from the parent function to
`f(x)=(x+5)^2+3`.

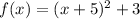Let us recall translation rules.

Horizontal translation:

`f(x)\rightarrow f(x-a)=\text{Graph shifted to right by a units}`

`f(x)\rightarrow f(x+a)=\text{Graph shifted to left by a units}`

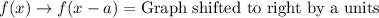
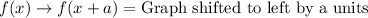
Vertical translation:

`f(x)\rightarrow f(x)-a=\text{Graph shifted downwards by a units}`

`f(x)\rightarrow f(x)+a=\text{Graph shifted upwards by a units}`

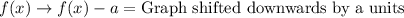
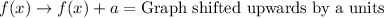
Upon looking at our given function, we can see that the value of 'a' is positive 5 inside parenthesis, so our graph is shifted to left by 5 units.

We can also see that the value of 'a' outside parenthesis is positive 3, therefore, the graph of parent function is shifted upwards by 3 units to get the graph of function
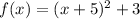`f(x)=(x+5)^2+3`.