Question

The area of the regular octagon is approximately 54 cm2. What is the length of line segment AB, rounded to the nearest tenth?

Answer 1

Answer:3.4

Explanation:

For enginuity- just took the test

Answer 2

AB = 3.3 cm

Explanation:

The formula to find out area of a regular octagon is given by

`A=2(1+√(2))a^(2)`

where a is the length of each side of the regular octagon.

Plugin A=54 into the formula

`54=2(1+√(2))a^(2)`

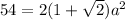
Divide both sides by 2

`(54)/(2) =(2)/(2) (1+√(2))a^(2)`

`27 = (1+√(2))a^(2)`

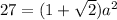
Plugin √2 as 1.41

`27 = (1+1.41)a^(2)`

`27 = (2.41)a^(2)`

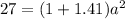
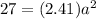
Divide both sides by 2.41

`(27)/(2.41) = (2.41)/(2.41) a^(2)`

`11.20 = a^(2)`

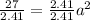
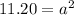
Taking square root on both sides

`√(11.20)  = \sqrt{a^(2)}`

a = 3.346

a = 3.3 cm (rounded to nearest tenth)

so, length of side AB = 3.3 cm