Question

Point P is the center of two concentric circles. PQ = 4.2 and PS = 8.2. mc027-2.jpg is tangent to the smaller circle and a chord of the larger circle. What is length to the nearest tenth?

Answer 1

14.08 which rounds to 14.1

Answer 2

The length of the chord is 14.1 units.

Explanation:

Given : Two concentric circles with common center Point P.

Smaller circle with radius, PQ = 4.2 unit

Bigger circle with radius, PS = 8.2 unit

Tangent to the smaller circle is a chord of the larger circle.

To find: Length of the chord , RS

Solution:

Perpendicular drawn from the center of the circle to the chord bisect the chord. So,

SQ = QR

In given figure, ΔPSQ

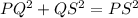`PQ^2+QS^2=PS^2` (Pythagoras theorem)

`(4.2 unit)^2+QS^2=(8.2 unit)^2`

`QS=7.042 units`

RS = SQ + QR = 7.042 units+7.042 units = 14.084 units ≈ 14.1 units.

The length of the chord is 14.1 units.