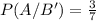According to the general equation for conditional probability, if P(A and B^)= 1/6 and P(B')= 7/18, what is P(A and B') ?

Question

asked Sep 1, 2018 24.6k views

2 Answers

Edouard Thiel · Answer 1 · 2018-09-07T19:44:13+0000

Answer:

The required probability is
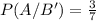
P(A/B')=(3)/(7)

Explanation:

Given :
$\text{P(A and }B')=(1)/(6)$ and
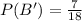
P(B')=(7)/(18)

To find : What is P(A/B') ?

Solution :

The conditional probability states that,

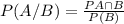
$P(A/B)=(PA\cap B)/(P(B))$

According to given situations,

The conditional probability is

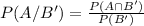
$P(A/B')=(P(A\cap B'))/(P(B'))$

Substitute
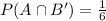$P(A\cap B')=(1)/(6)$ and
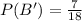
P(B')=(7)/(18)

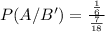
P(A/B')=((1)/(6))/((7)/(18))

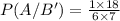
P(A/B')=(1* 18)/(6* 7)

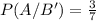
P(A/B')=(3)/(7)

Therefore, The required probability is
P(A/B')=(3)/(7)