Solution
Step 1
![\begin{gathered} \mathrm{Critical\:points\:are\:points\:where\:the\:function\:is\:defined\:and\:} \\ \begin{equation*} \mathrm{its\:derivative\:is\:zero\:or\:undefined} \end{equation*} \end{gathered}]()
Step 2
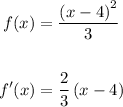
Step 3
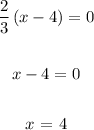
Critical point is x = 4
Step 4
Concavity intervals definition
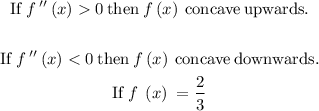
Step 5
[tex]\mathrm{Concave\:Upward}:-\infty \:Final answer
[tex]\begin{gathered} Critical\text{ }pointis\text{ }x=4 \\ \mathrm{Concave\:Upward}\text{ on interval:}-\infty\: