Answer with explanation:
To find the height of rope from other end of the equation,
h=0.01 x² - x + 27, where h is the height (in inches) above the ground and x is the distance (in inches) along the ground measured from the horizontal position of one end.
We will Substitute,
h=0,and get ,two roots of the Quadratic function.
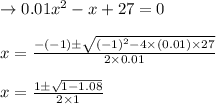
→→For a quadratic function of the type, ax² +b x +c=0
Roots can be obtained by the formula
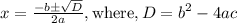
As the two roots obtained are not real.
It will not cut the x axis.
Now, finding the vertex of the parabola,which has coordinate, (50,2).
→Lowest part of the rope is 2 inches above the ground.
For,the quadratic function
→y=0.01 x² - x + 27
→ y =0.01×(x² -100 x + 2700)
→y = 0. 01 ×[(x-50)²-2500+2700]
→y -2 = 0.01 (x-50)²
⇒Vertex = (50,2)
h=2 inches→→Lowest part of the rope above the ground.