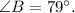Answer:
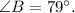
Explanation:
When two lines cross each other , then the opposite angles are known as vertical angles.
Vertical angles are equal.
Here, ∠A and ∠B are vertical angles.
So, ∠A = ∠B
If
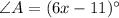 and
and
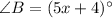
Then ,
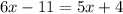
Subtract 5x from both sides, we get
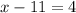
Add 11 on both sides, we get
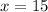
Now ,
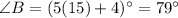
Hence, the measure of