Question

A sphere fits snugly inside a cube with 6-in. edges. what is the approximate volume of the space between the sphere and cube to the nearest whole number?

Answer 1

Volume of cube=s^3
s=6
V of cube=216
Volume of sphere=(4/3)pi(r^3)
r=3, if diameter=6
(4/3)(pi)(3^3)
V of sphere=36pi
Vcube-Vsphere=102.9026645
=103

Answer 2

103 cube inches

Explanation:

Since sphere fits snugly inside a cube therefore diameter of sphere will be equal to side of the cube [ which is given to be 6 inches ]

diameter = 6 inches

radius =
`(diameter )/(2)`

=
`(6 )/(2)`

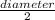
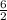
= 3 inches

Volume of the sphere is given by
`(4)/(3)\pi r^3`

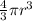
here r =3 inches

therefore volume is=
`(4)/(3)\pi 3^3`

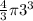
= 36 pi

= 36 ( 3.142)

= 113.097 cube inches

Volume of Cube = side x side xside = 6x6x6 = 216 cube inches

Volume of space between sphere and cube = 216 - 113.097= 102.9 cube inches , nearest whole number is 103 cube inches