Question

Simplify 5 to the 5th over 5 to the 8th.

1 over 5 to the 3rd power
53
1 over 25
1 over 5 to the negative 3rd

Answer 1

5^5/5^8
First of all, to simplify this ,we need to know about Law of Exponent rule which is:
a^p/a^q
=a^p-q (a≠0)
Now, we just do the same thing with this:
5^5/5^8
=5^5-8
=5^-3
Also, to make this simple, apply this into another Law of Exponents which is:
a^-p
=1/a^p (a≠0)
To the same to this
5^-3
=1/5^3. As a result, 1 over 5 to the 3rd power is your final answer. Hope it help!

Answer 2

The correct option is A) 1 over 5 to the 3rd power.

Explanation:

Consider the provided information.

5 to the 5th over 5 to the 8th

This can be written as:

`(5^5)/(5^(8))`

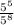
Now, use the property of exponent:
`(a^m)/(a^n)=a^(m-n)`

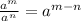
Use the above property to solve the provided expression.

`5^(5-8)`

`5^(-3)`

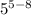
Negative exponent rule:
`a^(-m)=(1)/(a^m)`

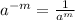
Use the above rule as shown:

`5^(-3)`

`(1)/(5^(-3))`

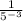
Thus, the simplified form of the provided expression is
`(1)/(5^(-3))`.

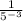Hence, the correct option is A) 1 over 5 to the 3rd power.