Question

Given the graph of y = f(x), explain and contrast the effect of the constant c on the

graphs of y = f(cx) and y = cf(x).

Answer 1

We use the graph of
`f(x)=sin(x)` as an example. The graph is shown in the first picture below

Let's take 2 as the value of the constant 'c'

The transformation of
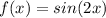
`f(x)=sin(2x)` gives the effect of halving the x-coordinates, as shown in the second picture.

The transformation of
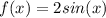
`f(x)=2sin(x)`, as shown in the third picture, gives the effect of doubling the y-coordinate

In conclusion,
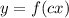
`y=f(cx)`gives the effect of halving the x-coordinates while
`y=cf(x)` gives the effect of doubling the y-coordinates