Answer:
9.8°
Step-by-step explanation:
We can model the situation as follows:
So, we need to calculate the value of x.
The sides of the triangle and the angle x are related by the following trigonometric function:

Therefore, we can solve for x, using the inverse function of tangent as follows:
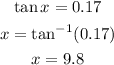
Then, the angle of depression is 9.8°