Answer: The solpes of the two equations are same but y-intercepts are different.
Step-by-step explanation: Given that Melanie uses the ordered pairs (2010, 48) and (2013, 59) to find her equation.
Tracy defines x as the number of years since 2010 and uses the ordered pairs (0, 48) and (3, 59) to find her equation.
We are to compare the equations of Melanie and Tracy.
Since both the girls used two points to find their equations, so the graph of the equations must be straight lines.
Melanie's Equation: Since two points in Melanie's equation are (2010, 48) and (2013, 59), so the slope of the line will be
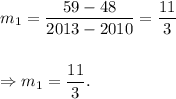
Therefore, Melanie's equation is
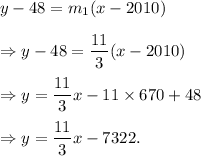
Tracy's Equation: Since two points in Tracy's equation are (0, 48) and (3, 59), so the slope of the line will be
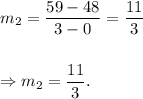
Therefore, Tracy's equation is
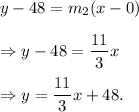
Thus, we can see that
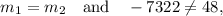
so, the slopes of two equations are same but y-intercepts are different.