Given a dilation with the origin O (0, 0), by observation determine the scale factor "K." DO, K = (5, 0) (10, 0) The dilation an expansion. True False

Question

asked Aug 7, 2018 32.6k views

2 Answers

Nirbhay Rana · Answer 1 · 2018-08-12T16:31:58+0000

Answer:

The scale factor is 2 and the statement "The dilation an expansion" is true.

Explanation:

The center of dilation is origin and dilation is rule is given as

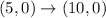
$(5,0)\rightarrow (10,0)$

The dilation with scale factor k with the center of dilation at origin is defined as

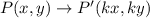
$P(x,y)\rightarrow P'(kx,ky)$

If k>1, then it is an expansion and if k<1, then it is a compression.

The formula for scale factor is

$k=\frac{\text{x-coordinate of image}}{\text{x-coordinate of preimage}}$

k=(10)/(5)

k=2

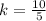
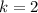
The scale factor is 2.

Since 2>1, therefore the given dilation is an expansion.

The scale factor is 2 and the statement "The dilation an expansion" is true.