Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s). Six times Jason's collection of books and one-third of Nathan's collection add up to 134 books. One-third of Jason's collection and Nathan's entire collection add up to 31 books. The number of books in Jason's collection is (Answer here) , and the number of books in Nathan's collection is (answer here) .

Answer 1

Answer: The number of books in Jason's collection = 21

The number of books in Nathan's collection = 24.

Explanation:

Let the number of books Jason has be 'J'.

Let the number of books Nathan has be 'N'.

According to question, we have ,

`6J+(1)/(3)N=134\\\\18J+N=134* 3=402\\\\18J+N=402---------(1)`

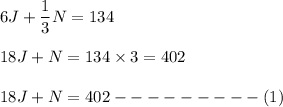
Similarly, we have,

`(1)/(3)J+N=31\\\\J+3N=31* 3\\\\J+3N=93-----------(2)`

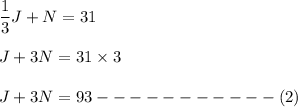
So, graphically, we get the values of J and N:

The number of books in Jason's collection = 21

The number of books in Nathan's collection = 24.

Answer 2

Based on the given above, collection of books of Nathan and Jason can be translated into the following equations:
6J + 1/3N = 134
1/3 J + N = 31; J = Jasons and N=Nathan
Solving two equations with two unknowns simultaneously,
Jason = 21 books and Nathan = 24 books