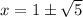Answer:
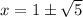
Explanation:
Equation:
 --1
--1
Quadratic formula :
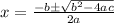
Now Solve the given option using this formula
A)
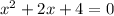
On comparing with 1
a = 1 , b = 2 , c= 4
So,

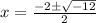
B)
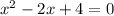
On comparing with 1
a = 1 , b = -2 , c= 4
So,

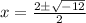
C)
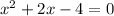
On comparing with 1
a = 1 , b = 2 , c=- 4
So,
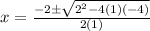
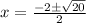
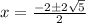
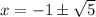
D)

On comparing with 1
a = 1 , b = -2 , c= -4
So,
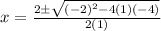
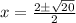
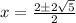
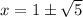
Hence Option D is correct.
 has a solution
has a solution