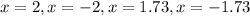Question

What are the roots of the polynomial equation x4+x2=4x3-12x+12? use a graphing calculator and a system of equations. round no integer roots to the nearest hundredth

-12
–2.73, 2.73
–1.73, 1.73
12

Answer 1

I think the answer is c but i may be wrong, try using desmos online graphing calculator

Answer 2

`x = 2, x =-2, x = 1.73, x = -1.73`

Explanation:

We are given the equation:

`x^4+x^2=4x^3-12x+12\\x^4-4x^3+x^2+12x-12=0`

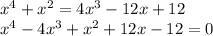
The attached image shows the graph for the given equation.

We can also factorize the given equation in the following manner.

By hit and trial method, we checked that 2 is a root of the given equation, that is,

`(2)^4-4(2)^3+(2)^2+12(2)-12 = 0`

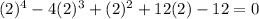
Thus, we can write:

`(x-2)(x^3-2x^2-3x+6 ) = 0\\(x-2)(x^2(x-2)-3(x-2)) = 0\\(x-2)(x-2)(x^2-3) = 0\\(x-2)(x-2)(x-\sqrt3)(x+\sqrt3)=0\\x=2,x=-2, x = \sqrt3, x = -\sqrt3`

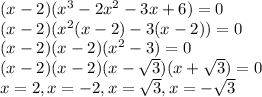
Thus, the roots of given equation are:

`x = 2, x =-2, x = 1.73, x = -1.73`