Question

What are the vertical and horizontal asymptotes of f(x)=2x/x-1

a. horizontal asymptote at y = 0, vertical asymptote at x = 1
b. horizontal asymptote at y = 2, vertical asymptote at x = 1
c. horizontal asymptote at y = 1, vertical asymptote at x = 0
d. horizontal asymptote at y = 1, vertical asymptote at x = 2

Answer 1

Answer is B

Explanation:

Answer 2

Find the vertical and horizontal asymptotes of the graph of the function
`f(x)=(2x)/(x-1):`

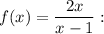
1. Vertical asymptote.

Since the denominator of the fraction is
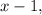`x-1,` then the vertical asymptote is
`x=1,` because the domain of the function is
`x\\eq 1.`

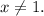
2. Horizontal asymptote.

Rewrite the function f(x):

`f(x)=(2x)/(x-1)=(2x-2+2)/(x-1)=(2(x-1)+2)/(x-1)=2+(2)/(x-1).`

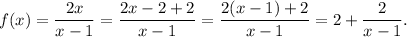
The horizontal asymptote has the equation
`y=2.`

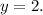
Answer: correct choice is B