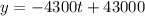Question

A business uses straight-line depreciation to determine the value y of a piece of machinery over a 10-year period. Suppose the original value (when t=0) is equal to $43,000 and its value is reduced by $4300 each year. Write the linear equation that models the value y of this machinery at the end of year t.

Answer 1

Suppose the original value​ (when t​=0) is equal to ​$34,000 and its value is reduced by ​$3400

Answer 2

Since two points define a line, we can take two points through which the line passes and find its equation.

From the word problem, we know that when t = 0, the original value is equal to $43,000. Then, we have a first ordered pair.

`(0,43000)`

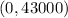
Since the value is reduced by $4300 each year, we have a second ordered pair.

`\begin{gathered} 43000-4300=38700 \\ (1,38700) \end{gathered}`

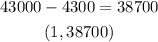
Now, we find the slope of the line using the following formula.

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1)) \\ \text{ Where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`
`\begin{gathered} (x_1,y_1)=(0,43000) \\ (x_2,y_2)=(1,38700) \\ m=(38700-43000)/(1-0) \\ m=(-4300)/(1) \\ m=-4300 \end{gathered}`

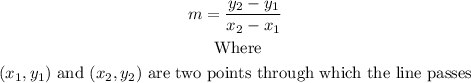
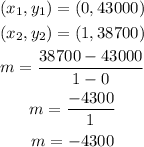
Finally, we can use and solve for y the point-slope formula.

`y-y_1=m(x-x_1)\Rightarrow\text{ Point-slope formula}`

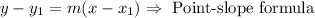
Since the situation described depends on the time t, we replace x with t in the formula.

`\begin{gathered} y-43000=-4300(t-0) \\ y-43000=-4300t \\ \text{ Add 43000 from both sides} \\ y-43000+43000=-4300t+43000 \\ y=-4300t+43000 \end{gathered}`

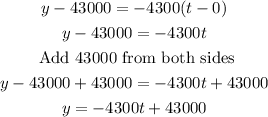
Therefore, the linear equation that models the value y of the machinery at the end of year t is:

`y=-4300t+43000`