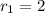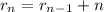Question

Find the recurrence relation satisfied by rn, where rn is the number of regions that a plane is divided into by n lines, if no two of the lines are parallel and no three of the lines go through the same point.

Answer 1

1. Take a look at the pictures attached.

2.

i) the first line divides the plane into 2 regions

ii) the second line adds 2 more regions so we have 4 in total.

iii) the third line adds 3 more regions, so 4+3=7 regions

iv) the fourth line adds 4 more regions.

so the
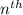
`n^(th)` line adds n more regions to the ones created by the previous n-1 lines.

3.


`r_1=2`


`r_2=2+2=4`


`r_3=4+3=7`


`r_4=7+4=11`


`r_n=r_n_-_1+n`

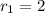
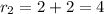
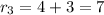
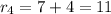
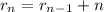
So the recurrence relation is


`r_1=2`

`r_n=r_n_-_1+n`