Question

Indicate the equation of the line meeting the given conditions. Please put the equation in standard form. Containing A(1, 3) and B(0, 2)

Answer 1

M = y2-y1/x2-x1
= 2 - 3 / 0 - 1
= -1 / -1
= 1

Y = x + b
2 = 0 + b
2 = b

Y = x + 2
0 = x - y + 2
-2 = x - y
2 = -x + y

Therefore, the equation of the line in standard form is 2 = -x + y

(not sure if done right lol)

Answer 2

`x-y=-2`

Explanation:

The standard form of a line is given by:

`Ax+By=C\\\\A,B,C \in R`

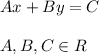
Given a point:

`P_1=(x_1,y_2)`

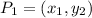
and a slope
`m`:

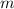The equation of the line can be obtained in a simple way from the point-slope formula:

`y-y_1=m(x-x_1)`

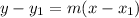
The slope of a line is defined as the difference on the y-axis divided by the difference on the x-axis for two different points on a line:

`m=(\Delta y)/(\Delta x) =(y_2-y_1)/(x_2-x_1)`

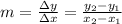
So, given the points:

`P_1(x_1,y_1)=A(1,3)\\P_2(x_2,y_2)=B(0,2)`

The slope is:

`m=(2-3)/(0-2) =(-1)/(-1)=1`

Now, using the point
`A(1,3)`:

`y-3=1(x-1)\\\\y-3=x-1\\\\y=x-1+3\\\\y=x+2`

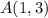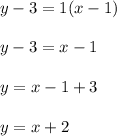
Finally, let's rewrite the obtained expression in its standar form:

`x-y=-2`