Question

PLEASE HELP A deck of playing cards has four suits, with thirteen cards in each suit consisting of the numbers 2 through 10, a jack, a queen, a king, and an ace. The four suits are hearts, diamonds, spades, and clubs. A hand of five cards will be chosen at random.

Which statements are true? Check all that apply.
The total possible outcomes can be found using 52C5.

The total possible outcomes can be found using 52P5.

The probability of choosing two diamonds and three hearts is 0.089.

The probability of choosing five spades is roughly 0.05

The probability of choosing five clubs is roughly 0.0005.

Answer 1

The first option and the last option

Answer 2

1 and 5 is true

Explanation:

Given : A deck of playing cards has four suits, with thirteen cards in each suit consisting of the numbers 2 through 10, a jack, a queen, a king, and an ace. The four suits are hearts, diamonds, spades, and clubs.

Total no. of cards = 52

We are given that A hand of five cards will be chosen at random.

So, Number of Possible outcomes =
`^(52)C_5`

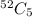
Thus Statement 1 is true

Statement 2 is false because in permutation sequence is considered .

We are not given any sequence of card for drawing 5 cards.

So, Statement 2 does not applies here .

Number of diamonds = 4

So, probability of choosing two diamonds and three hearts in draw of five cards :

=
`(13)/(52) * (12)/(51) * (13)/(50) * \frac{12}[49} * (11)/(48)`

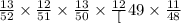
=0.00085

Thus Statement 3 is false.

Total spades = 13

Probability of choosing 5 spades=
`(13)/(52) * (12)/(51) * (11)/(50) * \frac{10}[49} * (9)/(48)`=0.000495

Statement 4 is false.

Total no. of clubs = 13

Probability of choosing 5 clubs=
`(13)/(52) * (12)/(51) * (11)/(50) * \frac{10}[49} * (9)/(48)`=0.000495 ≈0.0005

Statement 5 is true.