Question

How do I solve this?

Rudy has been awarded some money in a settlement. He has the option to take a lump sum payment of $200,000 or get paid an annuity of $1,000 per month for the next 25 years. Which is the better deal for Rudy, and by how much, assuming the growth rate of the economy is 2.75% per year?

1)
Lump Sum: by $14,899.82


2)
Annuity: by $14,899.82


3)
Annuity: by $43,535.88


4)
Lump Sum: by $43,535.88

Answer 1

Hi there

First find the present value of annuity ordinary THE formula is
PVAO= pmt [(1-(1+r)^(-n))÷(r)]
PMT 1000×12months=12000 per year
R interest rate 0.0275
N time 25 years
So
PVAO=12,000×((1−(1+0.0275)^(
−25))÷(0.0275))
=214,899.82

Now compare the result with the amount of the lump sum
214,899.82−200,000
=14,899.82

So the answer is
2) Annuity: by $14,899.82

Hope it helps

Answer 2

2) Annuity: by $14,899.82

Explanation:

Given is -

Rudy has been awarded some money in a settlement.

He has the option to take a lump sum payment of $200,000

or get paid an annuity of $1,000 per month for the next 25 years.

Lets assume, that the growth rate of the economy is 2.75% per year

We will find how much the value becomes in annuity after 25 years.

p =
`12000*12=12000`

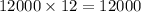
r = 0.0275

n = 25 years

Present value formula is =
`p(1-(1+r)^(-n) )/(r)`

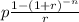
Putting the values in formula, we get

`12000(1-(1+0.0275)^(-25) )/(0.0275)`

=>
`12000(1-(1.0275)^(-25) )/(0.0275)`

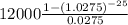
= $214900.36

Now the difference between annuity and lump sum =

`214900.36-200000=14900.36`

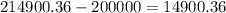
We can take this as, close to given option 2.

Therefore, option 2 is correct.

The better deal for Rudy is to get paid an annuity, as it will give him $14899.82 more in 25 years than the lump sum amount.