Question

The temperature of a cup of coffee varies according to Newton's Law of Cooling: , where T is the water temperature, A is the room temperature, and k is a positive constant.

If the coffee cools from 180°F to 100°F in 10 minutes at a room temperature of 75°F, how long (to the nearest minute) will it take the water to cool to 80°F?

Answer 1

Starting with:

`T = (T_0 - A) e^(-kt) + A`
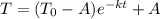
T0 is initial temperature of coffee ---> 180
A = 75

Step 1: Find value for k
plug in T = 100, t = 10 min

`100 = 105e^(-10k) + 75 \\ \\ (25)/(105) =(5)/(21)= e^(-10k) \\ \\ ((5)/(21))^(1/10) = e^(-k)`

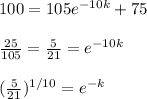
This is just as good as finding an actual value for 'k' because it will be subbed into Cooling equation anyway. Subbing in e^(-k) is easier.

Step 2: Find value for 't' when T = 80

`80 = 105 ((5)/(21))^(t/10) + 75 \\ \\ ((5)/(21))^(t/10) = (5)/(105) = (1)/(21) \\ \\ ((5)/(21))^t = ((1)/(21))^(10) \\ \\ ln((5)/(21))^t = ln((1)/(21))^(10) \\ \\ t = (10 ln((1)/(21)))/(ln((5)/(21))) = 21.21`

Therefore it takes about 21 minutes for coffee to cool from 180 to 80 degrees.