Answer:
Option A
Explanation:
Given that in triangle ABC AM is one median
D is the centroid
We know by triangle conjectures that
in any triangle centroid divides median in the ratio 2:1
i.e. If D is centroid on AM,
then AD:DM =2:1
Substitute for AD and DM the given values
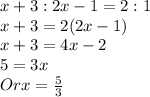
Hence answer is the length of AM
= AD+DM
=
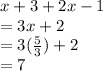
Option A is the answer