Question

Find cotθ if θ terminates in Quadrant III and secθ = - 2.

Answer 1

`\bf cot(\theta)=\cfrac{adjacent}{opposite}\qquad \qquad sec(\theta)=\cfrac{hypotenuse=c}{adjacent=a}\\\\ -------------------------------\\\\ sec(\theta)=-2\iff sec(\theta)=-\cfrac{2}{1} \cfrac{\leftarrow hypotenuse}{\leftarrow adjacent}`

so hmmm let's recall, the hypotenuse, or radius, is never negative, since it's just a unit of the radius, so from -2/1 the negative fellow has to be the denominator, namely, the adjacent side, so a = -1, c = 2

bear also in mind, the angle is in the III quadrant, and on that quadrant, the sign for the x-coordinate is negative, so is -1

so.. what's the opposite side? or b? let's use the pythagorean theorem then


`\bf c^2=a^2+b^2\implies \pm√(c^2-a^2)=b\implies \pm√((2)^2-(-1)^2)=b \\\\\\ \pm√(3)=b`

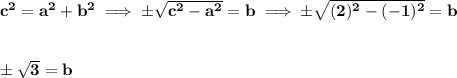
so.. which is it? the +/-? well, we're on the III quadrant, on there both the "x" and "y" coordinates are both negative, so "b" has to also be negative, thus -√(3)=b



`\bf cot(\theta)=\cfrac{adjacent}{opposite}\implies cot(\theta)=\cfrac{a}{b}\implies cot(\theta)=\cfrac{-1}{-√(3)} \\\\\\ cot(\theta)=\cfrac{1}{√(3)}\impliedby \textit{now, let's rationalize that}\\\\ -------------------------------\\\\ \cfrac{1}{√(3)}\cdot \cfrac{√(3)}{√(3)}\implies \boxed{\cfrac{√(3)}{3}}`