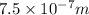Answer: The wavelength of the wave travelling through vaccum is
Step-by-step explanation:
To calculate the wavelength of the wave, we use the formula:
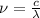
Rearranging the terms,
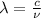
Where,
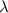 = wavelength of the wave = ?
= wavelength of the wave = ?
 = Frequency of the wave =
= Frequency of the wave =
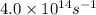
c = Speed of light in vacuum =
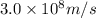
Putting values in above equation, we get:
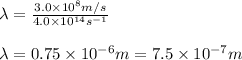
Hence, wavelength of the wave in vacuum will be