Question

Newton's Method: Calculus I need assistance and a clear explanation so I can understand. Please be clear

Answer 1

Newtons method is a way to approximate the zero of a function.
It is a recursive method such that the output becomes the new input, the goal is to approach the zero by having the inputs change by a smaller amount each iteration until that change is nearly 0.

First, let me explain where the method comes from.
The formula is really just a manipulation of the slope formula using 2 points; the point tangent to the curve, and the point where the tangent line crosses the x-axis.
If (x,y) is point on curve, then (x*,0) is point on tangent line at x-axis.

`m = (dy)/(dx) = (y - 0)/(x - x^*)`

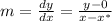
Rearranging for x*:

`x^* = x - (y)/(dy/dx)`

This is the formula for newtons method. y = f(x), dy/dx = f'(x)
Now what happens is (x*,y*) becomes new point on curve with new tangent line with different slope.
This new line will cross x-axis at different point x** and so on until eventually f(x) gets really really close to 0.

Now for the example:
you need to take derivative f'(x) using product rule:

`f(x) = x tan(x) - 1 \\ \\ f'(x) = tan(x) + x sec^2 (x)`

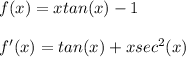
Then its just a matter of plugging in values for x, and repeating until we get close to a zero.

First plug in x = 1

`x_1 = 1 - ((1)(tan 1) - 1)/(tan 1 + (1)sec^2 (1)) = 0.888136 \\ \\ x_2 = .888136 - (f(.888136))/(f'(.888136)) = 0.861465 \\ \\ x_3 = .861465 - (f(.861465))/(f'(.861465)) = 0.860335 \\ \\ x_4 = .860335 - (f(.860335))/(f'(.860335)) = 0.860334 \\ \\ x_5 = .860334 - (f(.860334))/(f'(.860334)) = 0.860334`

Now we can stop because x5 = x4 to 6 decimals, this means f(x) is very close to 0 and will serve as a good approximation for a solution.

Final Answer:
x = 0.860334