ANSWER
Step-by-step explanation
Events A and B are independent events if and only if
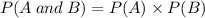
We were given that, the probability of getting disease X, which is event A is,
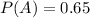
and the probability of getting disease Y, which is event B, is
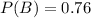
and
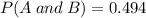
Now, let us find the probability of getting both disease X and Y,
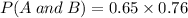
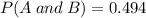
Since
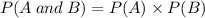
The two events are independent. Therefore A and B are independent events.