Question

JKL has vertices at J(-4,-2) K(1,-1) and L (-2,-4). Determine if JKL is a right triangle.

Answer 1

Yes, it is a right triangle

Explanation:

Hello, I think I can help you with this

you can solve this finding the lengths and then find the longest length, it would be the hypotenuse, and the lengths must fit to

`side^(2)+side^(2)=hypotenuse^(2)`

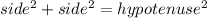
Step 1

you can find the distance between 2 points P1 and P2 using:

`\sqrt{(x_(1)-x_(2))^(2)+(y_(1)-y_(2))^(2) } \\where\\P1(x_(1),y_(1))\\ P2(x_(2),y_(2))\\\\`

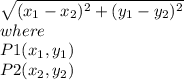
Let

P1=J(-4,-2)

P2=K(1,-1)

P3=L(-2,-4)

distance JK=P1P2=

`\sqrt{(x_(1)-x_(2))^(2)+(y_(1)-y_(2))^(2) } \\\sqrt{(-4-1)^(2)+(-2-(-1))^(2) } \\\sqrt{(-5)^(2)+(-1))^(2) } \\√(25+1) \\√(26) =5.09\ units`

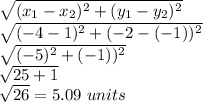
distance KL=P2P3=

`\sqrt{(x_(2)-x_(3))^(2)+(y_(2)-y_(3))^(2) } \\\sqrt{(1-(-2))^(2)+(-1-(-4))^(2) } \\\sqrt{(3)^(2)+(3)^(2) } \\√(9+9) \\√(18) =4.24\ units`

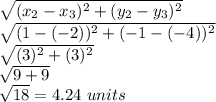
distance JL=P1P3=

`\sqrt{(x_(1)-x_(3))^(2)+(y_(1)-y_(3))^(2) } \\\sqrt{(-4-(-2))^(2)+(-2-(-4))^(2) } \\\sqrt{(-2)^(2)+(2)^(2) } \\√(4+4) \\√(8) =2.82\ units`

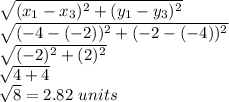
so the lengths are

`JK=√(26)\\KL=√(18) \\JL=√(8)`

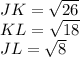
The longest length is JK, hence this is the hypotenuse

Step 2

Check

`side^(2)+side^(2)=hypotenuse^(2)\\(√(18) )^(2) +(√(8) )^(2) =(√(26) )^(2) \\18+8=26\\26=26,true`

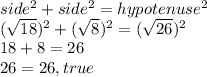
hence this is a right triangle.

Have a nice day