Question

The random variable R has the binomial distribution B (12,0.35) .find P(R>4)

Answer 1

Answer:
`0.416655`

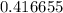
Explanation:

If random variable X has the binomial distribution B(n, p), then

`P(X=x)=\ ^nC_xp^x(1-p)^(n-x)`

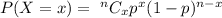
, where n= Total number of trials, x = number of successes , p= probability of success in each trial.

Given: The random variable R has the binomial distribution B (12,0.35).

n= 12, = 0.35

`P(R>4)=1-P(R\leq4)\\\\=1-[P(R=0)+P(R=1)+P(R=3)+P(R=4)]\\\\\\=1-[^(12)C_0(0.35)^(0)(1-0.35)^(12)+^(12)C_1(0.35)^(1)(1-0.35)^(11)+^(12)C_2(0.35)^(2)(1-0.35)^(10)+^(12)C_3(0.35)^(3)(1-0.35)^(9)+^(12)C_4(0.35)^(4)(1-0.35)^(8)]\\\\= 1-[(1)(0.65)^(12)+(12)(0.35)(0.65)^(11)+(12!)/(2!10!)(0.35)^2(0.65)^(10)+(12!)/(9!3!)(0.35)^3(0.65)^(9)+(12!)/(8!4!)(0.35)^4(0.65)^(8)]\\\\=1-0.583345\\\\\approx0.416655`

Hence, P(R>4)=0.416655