Answer:
Explanation:
Given a quadratic function,
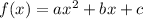
The leading term a>0 and also vertex has y coordinate 0
Since y coordinate is 0, vertex lies on x axis.
Since leading coefficient is positive, the parabola is open upward touching the x axis.
Since the parabola touches the x axis, we find that there are two equal roots for this equation.
i.e. there is one real zero with multiplicity 2.