First, we are going to solve the equation
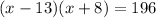 to find the value of
to find the value of
 .
.
Let's solve the equation step by step
Step 1. Use the distributive property to destroy the parenthesis:
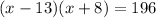
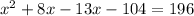
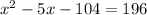
Step 2. Subtract 196 to both sides of the equation:
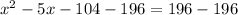
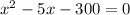
Step 3. Factor the expression:
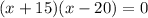
Step 4. Set each factor equal to zero and solve for
 :
:
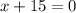 or
or
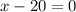
 or
or

Since we are dealing with lengths here, and lengths cannot be negative, the only valid solution is

Now, we know from our problem that the missing side of the rectangle is given by the expression
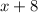 , so to find the actual length, we just need to replace
, so to find the actual length, we just need to replace
 with 8 in the given expression and simplify:
with 8 in the given expression and simplify:

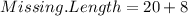
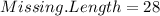 units
units
We can conclude that the missing side length represented by x + 8 units of the rectangle is 28 units.