The first equation is linear:
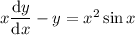
Divide through by
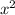
to get

and notice that the left hand side can be consolidated as a derivative of a product. After doing so, you can integrate both sides and solve for

.
![(\mathrm d)/(\mathrm dx)\left[\frac1xy\right]=\sin x](https://img.qammunity.org/2018/formulas/mathematics/college/qrei84de9ffse6cuyivsxiptjkkk241284.png)
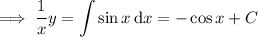
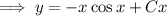
- - -
The second equation is also linear:
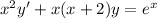
Multiply both sides by

to get

and recall that
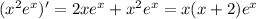
, so we can write

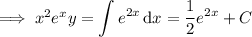

- - -
Yet another linear ODE:

Divide through by

, giving
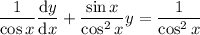

![(\mathrm d)/(\mathrm dx)[\sec x\,y]=\sec^2x](https://img.qammunity.org/2018/formulas/mathematics/college/6nqsnnmwh1fnv95zjyc1khpuw1ddif0ksm.png)
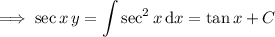
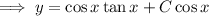
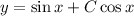
- - -
In case the steps where we multiply or divide through by a certain factor weren't clear enough, those steps follow from the procedure for finding an integrating factor. We start with the linear equation
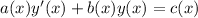
then rewrite it as

The integrating factor is a function

such that
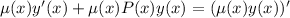
which requires that
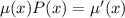
This is a separable ODE, so solving for
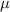
we have
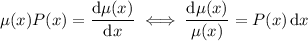
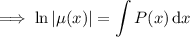
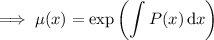
and so on.