Question

Determine the x-intercepts of the graph represented by the following quadratic function. Recall that y = f(x).f(x) = x2 − 4x − 21(x, y) = (smaller x-value)(x,y)= (larger x-value)

Answer 1

For this problem, we are given the expression for a quadratic equation and we need to determine the x-intercepts of its graph.

The x-intercepts coincide with the zeros of the equation, which are obtained when f(x) = 0. So we have:

`x^2-4x-21=0`

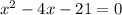
We need to determine the roots of the equation above.

`\begin{gathered} x_(1,2)=(-(-4)\pm√((-4)^2-4\cdot1\cdot(-21)))/(2\cdot1)\\ \\ x_(1,2)=(4\pm√(16+84))/(2)=(4\pm√(100))/(2)=(4\pm10)/(2)\\ \\ x_1=(4+10)/(2)=(14)/(2)=7\\ \\ x_2=(4-10)/(2)=(-6)/(2)=-3 \end{gathered}`

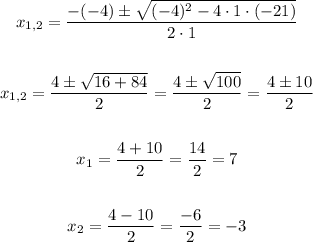
The intercepts are: (-3,0) and (7,0).