Question

write an equation, in factored form, of degree 6 polynomial that has four x-intercepts and a y-intercept of 64

Answer 1

f(x) = (3x-2)(x-3)(x-4)(x-2)^3

EXPLANATION :

A polynomial with a degree of 6 has 6 factors.

f(x) = (x - a)(x - b)(x - c)(x - d)(x - e)(x - f) with 6 roots or x-intercepts.

But the problems states that it has 4 x-intercepts, so we will reduced the number of roots but maintaining the number of factors.

f(x) = (x - a)(x - b)(x - c)(x - d)(x - a)(x - a).

From here, we still have 6 factors but only 4 x-intercepts, the last two factors (x - a) is the same as the first factor.

So we can rewrite this as :

`f(x)=(x-a)^3(x-b)(x-c)(x-d)`

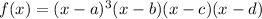
Next is to have a y-intercept of 64, y-intercept is the value of f(x) when x = 0

Substitute 0 to the function.

`\begin{gathered} f(0)=(0-a)^3(0-b)(0-c)(0-d) \\ f(0)=a^3(b)(c)(d) \end{gathered}`

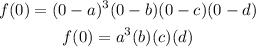
Now we have f(0) = a^3bcd and f(0) = 64 as the definition from above.

We need to find the factors of 64,

64 = 8 x 4 x 3 x 2/3

And we can rewrite the equation as :

`\begin{gathered} f(0)=a^3bcd \\ 64=a^3bcd \\ 8*4*3*(2)/(3)=a^3bcd \end{gathered}`

From here, we can observe that,

a^3 = 8 ⇒ a = 2

b = 4

c = 3

d = 2/3

So the function will be :

`\begin{gathered} f(x)=(x-2)^3(x-4)(x-3)(x-(2)/(3)) \\ f(x)=(x-2)^3(x-4)(x-3)(3x-2) \end{gathered}`

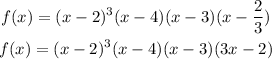
Explanation in 2/3

Since we only need 4 distinct factors of 64.

8 x 4 x 3 x 2/3

8 x 4 = 32

The product of the 3rd and 4th factor should be 2, in order to get 64.

Since from the first