Answer:
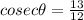 and
and
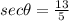
Explanation:
For the standard position triangle having sides of x=5 and y=12 and the included theta, the hypotenuse can be calculated through the Pythagorean theorem such as:
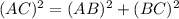
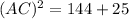
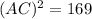
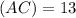
Therefore, the value of AC(Hypotenuse) is 13 units.
Now,
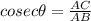
⇒
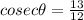
Also,
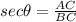
⇒
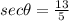
which are the required values of
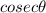 and
and
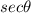 .
.