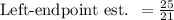We need to use the left endpoints as the length of each one of the four rectangles to estimate the area below the graph of
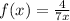
Since we need to divide the interval [1, 5] into four subintervals, the width of each rectangle will be 1:
Step 1
Find the height of the rectangles by evaluating f(x) at x = 1, 2, 3, and 4:
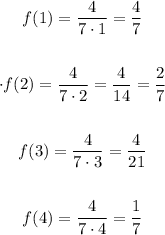
Step 2
Multiplying the height of each rectangle by its width (1), we find the areas of the rectangles. Since the widths are 1, the areas are numerically equal to the heights.
Then we add those areas to estimate the area between the curve and the x-axis in the interval [1, 5]:
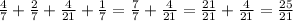
Answer
Therefore