Question

Quadrilateral KLMN is a rectangle. The coordinates of L are L(1,-4) and the coordinates of M are M(3,-2) find the slopes of sides KL,LM,MN,and NK

Answer 1

The slope of LM is 1, slope of KL is -1, slope of MN is -1 and the slope of NK is 1.

Explanation:

It is given that quadrilateral KLMN is a rectangle and the coordinates of L are L(1,-4) and the coordinates of M are M(3,-2).

If a line passing though two points, then the slope of the line is

`m=(y_2-y_1)/(x_2-x_1)`

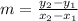
The slope of LM is

`m_(LM)=(-2-(-4))/(3-1)=1`

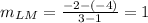
The slope of LM is 1.

Two consecutive sides of a rectangle are perpendicular and the product of slopes of two perpendicular lines are -1.

`m_(KL)* m_(LM)=-1`

`m_(KL)* 1=-1`

`m_(KL)=-1`

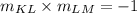
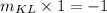
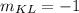
The slope of KL is -1.

The opposite sides of a rectangle are parallel and the slope of parallel lines are same.

Therefore, the slope of MN is -1 and the slope of NK is 1.

Answer 2

We can start by finding the gradient of LM

`m= ( y_(2)- y_(1) )/(x_(2) - x_(1) ) = (-2--4)/(3-1) = (2)/(2)=1`

Two perpendicular lines will meet the requirement
`m_(1)`×
`m_(2)`=-1
Two parallel lines have equal gradients

NM is perpendicular to LM, hence the gradient of NM is -1
KN is a line that is parallel to NM, hence the gradient is 1
KL is perpendicular to LM, hence the gradient of KL is -1