Question

Factor to find the zeros of the function defined by the quadratic expression.

12x2 − 156x + 480

Answer 1

12x2 − 156x + 480

Factor out the GCF: 12(x2 − 13x + 40)

Then, set to zero.

12(x2 − 13x + 40) =0
12(x − 8)(x − 5) = 0
x = 8 or x = 5

Answer 2

The zeroes of the quadratic function are 8 and 5.

Explanation:

The given quadratic expression is

`12x^2-156x+480`

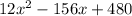
Taking out the greatest common factor from each term.

`12(x^2-13x+40)`

The middle term can be written as -8x-5x.

`12(x^2-8x-5x+40)`

`12(x(x-8)-5(x-8))`

`12(x-8)(x-5)`

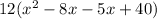
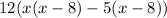
The factor form of the given expression is 12(x-8)(x-5). Equate the factors form equal to zero, to find the zeroes of the given expression.

`12(x-8)(x-5)=0`

Using zero product property, we get

`x=8,5`

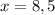
Therefore the zeroes of the quadratic function are 8 and 5.