Question

In triangle FGH, GJ is an angle bisector of ∠G and perpendicular to FH. What is the length of FH? units

Answer 1

The answer is C. on edgen.

Explanation:

C. 16

Answer 2

We know that line GJ bisects the angle FGH, that means we also know that the angle FGH is divided into two equal sizes.

Now, we have
Angle FGJ = Angle HGJ
Angle GJF = Angle GJH

This information means that angle GHJ = angle GFJ

We have two congruent right-angled triangle

We can then further deduce that
Side GF = Side GH

`3x-8=16`

`3x=16+8`

`3x=24`

`x=8`

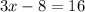
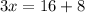
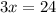
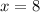
Since triangle FGJ and triangle GJH are congruent, then side FJ equals to side JH

Hence, the length of FH = 2×8=16