Question

You have two alcohol solutions: one with a concentration of 80%

Answer 1

8 liters of the first solution and 4 liters of the second solution.

Step-by-step explanation

The equations that govern the situation have been given as:

`\begin{gathered} A+B=12 \\ 0.8A+0.5B=8.4 \end{gathered}`

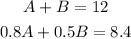
where A represents the amount of the first solution and B represents the amount of the second solution.

From the first equation, we can make A the subject of the formula:

`A=12-B`

Substitute that into the second equation:

`\begin{gathered} 0.8(12-B)+0.5B=8.4 \\ 9.6-0.8B+0.5B=8.4 \\ \Rightarrow-0.8B+0.5B=8.4-9.6 \\ -0.3B=-1.2 \\ B=(-1.2)/(-0.3) \\ B=4L \end{gathered}`

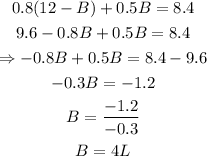
To find A, substitute the obtained value of B into the equation for A:

`\begin{gathered} A=12-4 \\ A=8L \end{gathered}`

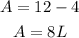
Hence, you would need 8 liters of the first solution and 4 liters of the second solution.