Based on the given information, the magnitude of the scalar multiple -2v is 13.416
How to find the magnitude of a scalar multiple
To find the magnitude of a scalar multiple, multiply each component of the vector by the scalar, and then calculate the magnitude of the resulting vector.
Given:
u = (2, 0)
v = (-3, 6)
We want to find the magnitude of the scalar multiple -2v.
To obtain -2v, we multiply each component of v by -2:
-2v = (-2 * -3, -2 * 6)
= (6, -12)
Now, we calculate the magnitude of -2v:
||-2v|| =
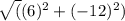
=
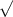 (36 + 144)
(36 + 144)
=
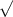 (180)
(180)
= 2 *
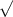 (45)
(45)
= 2 *
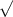 (9 * 5)
(9 * 5)
= 2 * 3 *
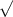 5
5
= 6 *
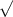 5
5
= 13. 416
Therefore, the magnitude of the scalar multiple -2v is 13.416