Question

The sides of a rhombus with angle of 60° are 6 inches. Find the area of the rhombus.

Answer 1

1. Check the drawing of the rhombus ABCD in the picture attached.

2. m(CDA)=60°, and AC and BD be the diagonals and let their intersection point be O.

3. The diagonals:
i) bisect the angles so m(ODC)=60°/2=30°

ii) are perpendicular to each other, so m(DOC)=90°

4. In a right triangle, the length of the side opposite to the 30° angle is half of the hypothenuse, so OC=3 in.

5. By the pythagorean theorem,
`DO= \sqrt{ DC^(2)- OC^(2) }= \sqrt{ 6^(2)- 3^(2) }=√( 36- 9 )=√( 27 )= √(9*3)=`

`=√(9)* √(3) =3√(3) (in)`

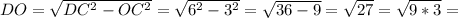
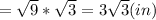
6. The 4 triangles formed by the diagonal are congruent, so the area of the rhombus ABCD = 4 Area (triangle DOC)=4*
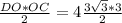
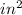
`(DO*OC)/(2)=4 (3 √(3) *3)/(2)`=
`=2*9 √(3)=18 √(3)` (
`in^(2)`)