Question

Nuclear medicine is a branchhh hof medicine which uses radioactive materials in diagnosis and therapy. Radioactive substances are administered to patients and the radiation emitted is measured. Iodine-131 which has a half-life of k days is a substance that is used to diagnose and treat cancers of thhhe thyroid gland. The graph below is an exponential decay for a dose(d) or iodine-131 given to a patient as a function in time in days.  

The graph shows the iodine remaining in body (% of dose) from 0-100 starting at 100. and the bottom of the graph is time(days from 0-60) and the graph is dropping with the marked point (24, 12.5) 

b) using the point (24, 12.5) , determine the half life k of iodine-131 and write the equation.

c)iodine 131 is unable to be detected after it has decayed 5% of its initial dose. Using your equation, determine how many days to the nearest tenth will have passed until the dose is undetectable?

I solved for b, need hhelp with C.

Answer 1

I'll just do it from the top just in case you didn't do something right

so,half life formula

A=P(1/2)^(t/k) where k is the half life and P is initial amount (or percent)

so, initial is 100
P=100

and, when t=24, A=12.5
so

solve for k

given
P=100
t=24
A=12.5
so

12.5=100(1/2)^(24/k)
divide both sides by 100
(12.5/100)=(1/2)^(24/k)
take ln of both sides
ln(12/5.100)=ln((1/2)^(24/k))
properties of logarithms
ln(12/5.100)=(24/k)ln(1/2)
times both sides by k
kln(12/5.100)=24ln(1/2)
divide both sides by ln(12.5/100)
k=(24ln(1/2))/(ln(12.5/1000))
use your calculator
k=8
exactly
so


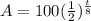
`A=100((1)/(2))^{(t)/(8)}` is da equation





c.
solving for t when A=5

so
A=5


`5=100((1)/(2))^{(t)/(8)}`
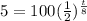
solve for t
divide oth sides by 100

`(5)/(100)=((1)/(2))^{(t)/(8)}`
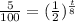
take ln of both sides

`ln((5)/(100))=ln(((1)/(2))^{(t)/(8)})`
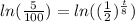
property of logarithm

`ln((5)/(100))=((t)/(8))ln((1)/(2))`
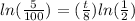
times both sides by 8 and divide both sides by ln(1/2)

`(8ln(5)/(100))/(ln(1)/(2)) =t`
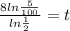
t≈34.5754
so to the tenth
34.6 days