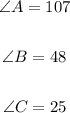Question

For the given triangle side AC=7, side BC= 9 and side AB=4.Part A: Find the measure of angle APart B: Find the measure of angle Bpart C: Find the measure of angle C

Answer 1

Step-by-step explanation:

Given;

We are given the following information for a triangle;

`AC=7,BC=9,AB=4`

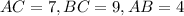
Required;

We are required to find the measures of angles A, B and C.

Step-by-step solution;

For any triangle with three sides given/available we can apply the cosine rule to calculate the missing angle(s).

The cosine rule is quoted below;

`\begin{gathered} a^2=b^2+c^2-2bcCosA \\ \\ OR \\ \\ b^2=a^2+c^2-2acCosB \\ \\ OR \\ \\ c^2=a^2+b^2-2abCosC \end{gathered}`

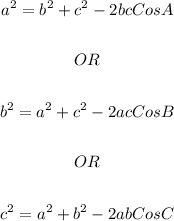
We shall now take angle A to begin with;

We start by making Cos A the subject of the equation;

`\begin{gathered} a^2=b^2+c^2-2bcCosA \\ Add\text{ }2bcCosA\text{ }to\text{ }both\text{ }sides: \\ \\ 2bcCosA+a^2=b^2+c^2 \\ \\ Subtract\text{ }a^{2\text{ }}from\text{ }both\text{ }sides: \\ \\ 2bcCosA=b^2+c^2-a^2 \\ \\ Divide\text{ }both\text{ }sides\text{ }by\text{ }2bc: \\ \\ CosA=(b^2+c^2-a^2)/(2bc) \end{gathered}`

With the refined form of the cosine formula we can now substitute and solve as follows;

`CosA=(7^2+4^2-9^2)/(2(7)(4))`
`\begin{gathered} CosA=(49+16-81)/(56) \\ \\ CosA=(-16)/(56) \\ \\ CosA=-0.285714285714 \end{gathered}`

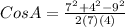
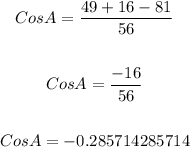
We can now use a calculator to find the value of arccos -0.2857...

`Cos^(-1)A=106.601549599`

Rounded to the nearest degree the angle measure is;

`\angle A=107\degree`

To solve for angle B, we can now apply the sine rule, since we have two sides and one of the angles. The sine rule is quoted below;

`(a)/(SinA)=(b)/(SinB)=(c)/(SinC)`

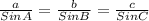
We have angle A, and side length a. We have side length b, which means we can solve for angle B. This is shown below;

`\begin{gathered} (a)/(SinA)=(b)/(SinB) \\ \\ Cross\text{ }multiply: \\ \\ SinB=(b* SinA)/(a) \end{gathered}`
`\begin{gathered} SinB=(7* Sin107\degree)/(9) \\ \\ SinB=(7*0.956304755963)/(9) \\ \\ SinB=0.743792587971 \end{gathered}`

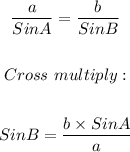
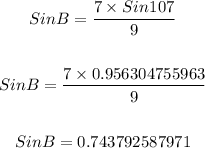
We can now use a calculator and find the arcsin of the decimal 0.7437...

`Sin^(-1)B=48.0554959457`

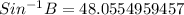
Rounded to the nearest degree, we now have;

`\angle B=48\degree`

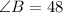
Note that the sum of angles in a triangle all sum up to 180 degrees.

We have angles A and B. We can calculate angle C as follows;

`\begin{gathered} \angle A+\angle B+\angle C=180 \\ \\ 107+48+\angle C=180 \\ \\ 155+\angle C=180 \end{gathered}`

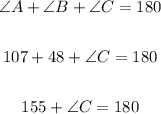
Subtract 155 from both sides;

`\angle C=25\degree`

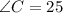
Therefore, the angles are;

ANSWER:

`\begin{gathered} \angle A=107\degree \\ \\ \angle B=48\degree \\ \\ \angle C=25\degree \end{gathered}`